Power Transfer Distribution Factors and Sensitivity Analysis#
Modern electricity markets rely on linearized models to quickly assess how power flows through the transmission network. This notebook bridges the gap between DC power flow theory and practical market applications by showing how to calculate Power Transfer Distribution Factors (PTDF) and related sensitivity factors from network topology data.
We’ll develop the mathematical foundation, implement the calculations from first principles, and demonstrate how these tools enable security-constrained economic dispatch (SCED) to handle transmission constraints and contingencies.
Setup and Data Preparation#
We’ll reuse the network data generation utilities from earlier notebooks but enhance them to properly specify bus types according to the MATPOWER convention.
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from pulp import *
# Set random seed for reproducibility
np.random.seed(42)
# Configure matplotlib
plt.style.use('seaborn-v0_8-darkgrid')
plt.rcParams['figure.figsize'] = (10, 6)
def create_network_with_bus_types():
"""Create 3-bus test network with proper bus type specification."""
# Bus data with MATPOWER convention: 1=PQ, 2=PV, 3=Slack
buses = pd.DataFrame({
'bus_id': [1, 2, 3],
'bus_type': [3, 1, 1], # Bus 1 is slack (type 3), others are PQ (type 1)
'demand': [0, 100, 80] # MW
}, index=['Bus1', 'Bus2', 'Bus3'])
# Generator data
generators = pd.DataFrame({
'bus': ['Bus1', 'Bus1', 'Bus3'],
'p_max': [200, 150, 150],
'cost': [20, 25, 22]
}, index=['G1', 'G2', 'G3'])
# Line data with electrical parameters
lines = pd.DataFrame({
'from_bus': ['Bus1', 'Bus1', 'Bus2'],
'to_bus': ['Bus2', 'Bus3', 'Bus3'],
'resistance': [0.02, 0.03, 0.025], # p.u.
'reactance': [0.1, 0.15, 0.2], # p.u.
'limit': [120, 100, 80] # MW
}, index=['L1', 'L2', 'L3'])
return buses, generators, lines
# Create our test network
buses, generators, lines = create_network_with_bus_types()
print("Bus Data:")
print(buses)
print("\nLine Data:")
print(lines[['from_bus', 'to_bus', 'reactance', 'limit']])
Bus Data:
bus_id bus_type demand
Bus1 1 3 0
Bus2 2 1 100
Bus3 3 1 80
Line Data:
from_bus to_bus reactance limit
L1 Bus1 Bus2 0.10 120
L2 Bus1 Bus3 0.15 100
L3 Bus2 Bus3 0.20 80
From DC Power Flow to PTDF#
The DC power flow model simplifies AC power flow by assuming:
All voltage magnitudes are 1.0 p.u.
Resistance is negligible compared to reactance (R << X)
Voltage angle differences are small (sin(θ) ≈ θ)
Under these assumptions, power flow on a line from bus i to bus j becomes:
The system of equations can be written in matrix form as:
where B is the susceptance matrix. To find how line flows respond to power injections, we need to:
Build the B matrix from network topology
Identify and handle the slack bus
Calculate sensitivities of line flows to bus injections
Building the B Matrix#
The B matrix (susceptance matrix) is constructed from the network topology. For DC power flow, we only consider the imaginary part of the admittance.
def build_b_matrix(buses, lines):
"""
Build the susceptance matrix (B matrix) for DC power flow.
Parameters:
-----------
buses : DataFrame
Bus data with bus_id and bus_type columns
lines : DataFrame
Line data with from_bus, to_bus, and reactance columns
Returns:
--------
B : numpy array
Susceptance matrix
bus_map : dict
Mapping from bus names to indices
"""
n_bus = len(buses)
B = np.zeros((n_bus, n_bus))
# Create bus name to index mapping
bus_map = {bus_name: i for i, bus_name in enumerate(buses.index)}
# Build B matrix from line data
for _, line in lines.iterrows():
i = bus_map[line['from_bus']]
j = bus_map[line['to_bus']]
b_ij = 1.0 / line['reactance'] # Susceptance = 1/reactance
# Off-diagonal elements (negative)
B[i, j] -= b_ij
B[j, i] -= b_ij
# Diagonal elements (positive)
B[i, i] += b_ij
B[j, j] += b_ij
return B, bus_map
# Build B matrix for our network
B, bus_map = build_b_matrix(buses, lines)
print("B Matrix (Susceptance Matrix):")
print(pd.DataFrame(B, index=buses.index, columns=buses.index).round(4))
print(f"\nMatrix properties:")
print(f"- Symmetric: {np.allclose(B, B.T)}")
print(f"- Singular (rows sum to 0): {np.allclose(B.sum(axis=1), 0)}")
B Matrix (Susceptance Matrix):
Bus1 Bus2 Bus3
Bus1 16.6667 -10.0 -6.6667
Bus2 -10.0000 15.0 -5.0000
Bus3 -6.6667 -5.0 11.6667
Matrix properties:
- Symmetric: True
- Singular (rows sum to 0): True
PTDF Calculation#
The Power Transfer Distribution Factor (PTDF) tells us what fraction of power injected at a bus flows through each line. To calculate PTDF:
Remove the slack bus from the B matrix (making it invertible)
Calculate voltage angle sensitivities to injections
Convert angle sensitivities to line flow sensitivities
The key insight is that PTDF[line, bus] = (θ_from - θ_to) / x_line when 1 MW is injected at bus.
def calculate_ptdf(buses, lines):
"""
Calculate PTDF matrix from network topology.
Parameters:
-----------
buses : DataFrame
Bus data with bus_type column (3 = slack bus)
lines : DataFrame
Line data with from_bus, to_bus, and reactance
Returns:
--------
ptdf : numpy array
PTDF matrix where ptdf[line_idx, bus_idx] is the fraction
of power injected at bus_idx that flows on line line_idx
slack_bus_idx : int
Index of the slack bus
"""
# Build B matrix
B, bus_map = build_b_matrix(buses, lines)
n_bus = len(buses)
n_line = len(lines)
# Find slack bus (bus_type == 3)
slack_mask = buses['bus_type'] == 3
if not slack_mask.any():
raise ValueError("No slack bus (type=3) found in bus data")
slack_bus_idx = np.where(slack_mask)[0][0]
slack_bus_name = buses.index[slack_bus_idx]
print(f"Slack bus identified: {slack_bus_name} (index {slack_bus_idx})")
# Create reduced B matrix (remove slack bus row and column)
non_slack_idx = [i for i in range(n_bus) if i != slack_bus_idx]
B_reduced = B[np.ix_(non_slack_idx, non_slack_idx)]
# Invert reduced B matrix
B_inv = np.linalg.inv(B_reduced)
# Build full sensitivity matrix (angles w.r.t. injections)
# This shows how voltage angles change with power injections
theta_sensitivity = np.zeros((n_bus, n_bus))
# Fill in sensitivities for non-slack buses
for j, j_reduced in enumerate(non_slack_idx):
for i, i_reduced in enumerate(non_slack_idx):
theta_sensitivity[j_reduced, i_reduced] = B_inv[j, i]
# Slack bus angle is always 0 (reference)
theta_sensitivity[slack_bus_idx, :] = 0
# Calculate PTDF from angle sensitivities
ptdf = np.zeros((n_line, n_bus))
for line_idx, (_, line) in enumerate(lines.iterrows()):
from_idx = bus_map[line['from_bus']]
to_idx = bus_map[line['to_bus']]
x_line = line['reactance']
# PTDF = (sensitivity of from_bus angle - sensitivity of to_bus angle) / reactance
# This represents the flow on the line per unit injection at each bus
for bus_idx in range(n_bus):
if bus_idx != slack_bus_idx:
ptdf[line_idx, bus_idx] = (
(theta_sensitivity[from_idx, bus_idx] -
theta_sensitivity[to_idx, bus_idx]) / x_line
)
# Slack row must be zero because of automatic balancing
ptdf[:, slack_bus_idx] = 0
return ptdf, slack_bus_idx
# Calculate PTDF for our network
ptdf, slack_idx = calculate_ptdf(buses, lines)
print("\nPTDF Matrix:")
ptdf_df = pd.DataFrame(ptdf,
index=[f"{l['from_bus']}-{l['to_bus']}" for _, l in lines.iterrows()],
columns=buses.index)
print(ptdf_df.round(4))
Slack bus identified: Bus1 (index 0)
PTDF Matrix:
Bus1 Bus2 Bus3
Bus1-Bus2 0.0 -0.7778 -0.3333
Bus1-Bus3 0.0 -0.2222 -0.6667
Bus2-Bus3 0.0 0.2222 -0.3333
Validating PTDF Properties#
A correctly calculated PTDF matrix must satisfy several important properties:
Each row should sum to zero (power is conserved)
Power injected at one bus and withdrawn at another should flow through the network
The flows should satisfy Kirchhoff’s current law at each bus
def validate_ptdf(ptdf, buses, lines):
"""
Validate PTDF matrix properties.
Key insight: PTDF columns show line flows when 1 MW is injected at a bus,
with the slack bus automatically providing balancing power.
"""
print("PTDF Validation:")
print("=" * 50)
# Property 1: Each row should sum to approximately zero
row_sums = ptdf.sum(axis=1)
print("1. Row sums (should be ≈ 0 for power conservation):")
all_zero = True
for i, line in enumerate(lines.index):
print(f" {line}: {row_sums[i]:.6f}")
if abs(row_sums[i]) > 1e-10:
all_zero = False
# Property 2: Test with a specific injection pattern
print("\n2. Test injection: 100 MW at Bus2")
print(" (Slack bus automatically provides -100 MW)")
# Find Bus2 index and slack
bus_map = {name: i for i, name in enumerate(buses.index)}
bus2_idx = bus_map["Bus2"]
slack_idx = np.where(buses["bus_type"] == 3)[0][0]
# PTDF already accounts for slack balancing, so just use the Bus2 column
line_flows = ptdf[:, bus2_idx] * 100
print(" Resulting line flows:")
for i, line in enumerate(lines.index):
print(f" {line}: {line_flows[i]:.2f} MW")
# Property 3: Verify Kirchhoff's current law
print("\n3. Power balance at each bus:")
for bus_name in buses.index:
bus_idx = bus_map[bus_name]
net_injection = 0
for line_idx, (_, line) in enumerate(lines.iterrows()):
if line["from_bus"] == bus_name:
# Power leaving this bus (positive)
net_injection += line_flows[line_idx]
elif line["to_bus"] == bus_name:
# Power entering this bus (negative)
net_injection -= line_flows[line_idx]
# Expected injection
if bus_name == "Bus2":
expected = 100
elif bus_idx == slack_idx:
expected = -100
else:
expected = 0
error = abs(net_injection - expected)
print(f" {bus_name}: Expected={expected:.0f} MW, Actual={net_injection:.1f} MW, "
f"Error={error:.6f} MW")
return all_zero
# Validate our PTDF matrix
validate_ptdf(ptdf, buses, lines)
PTDF Validation:
==================================================
1. Row sums (should be ≈ 0 for power conservation):
L1: -1.111111
L2: -0.888889
L3: -0.111111
2. Test injection: 100 MW at Bus2
(Slack bus automatically provides -100 MW)
Resulting line flows:
L1: -77.78 MW
L2: -22.22 MW
L3: 22.22 MW
3. Power balance at each bus:
Bus1: Expected=-100 MW, Actual=-100.0 MW, Error=0.000000 MW
Bus2: Expected=100 MW, Actual=100.0 MW, Error=0.000000 MW
Bus3: Expected=0 MW, Actual=0.0 MW, Error=0.000000 MW
False
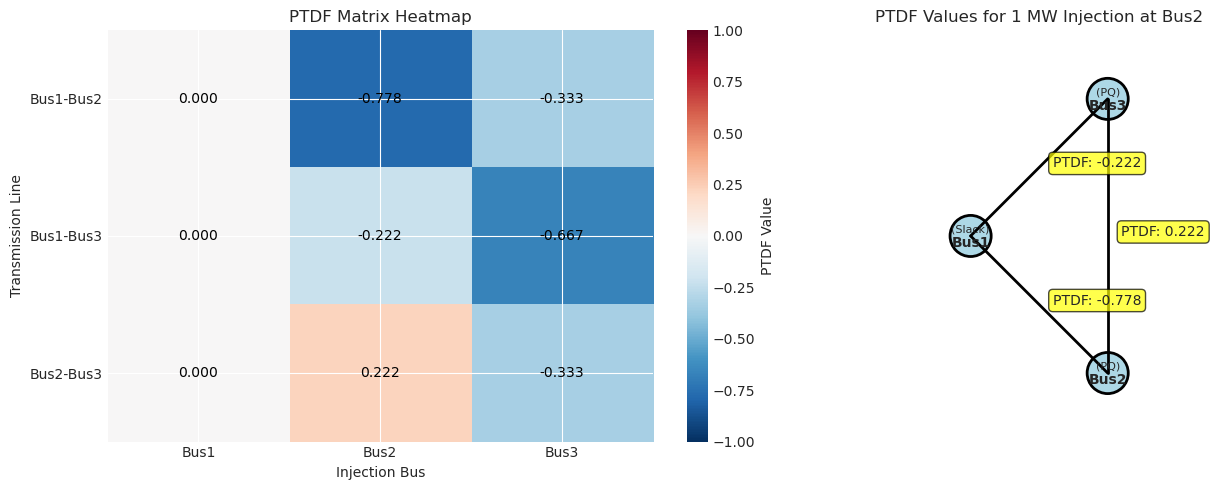
Visualizing PTDF#
Let’s visualize the PTDF matrix to better understand the sensitivity patterns.
# Visualize PTDF matrix
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(14, 5))
# Heatmap of PTDF values
im = ax1.imshow(ptdf, cmap='RdBu_r', vmin=-1, vmax=1, aspect='auto')
ax1.set_xticks(range(len(buses)))
ax1.set_xticklabels(buses.index)
ax1.set_yticks(range(len(lines)))
ax1.set_yticklabels([f"{l['from_bus']}-{l['to_bus']}" for _, l in lines.iterrows()])
ax1.set_xlabel('Injection Bus')
ax1.set_ylabel('Transmission Line')
ax1.set_title('PTDF Matrix Heatmap')
# Add values to heatmap
for i in range(len(lines)):
for j in range(len(buses)):
text = ax1.text(j, i, f'{ptdf[i, j]:.3f}',
ha="center", va="center", color="black", fontsize=10)
plt.colorbar(im, ax=ax1, label='PTDF Value')
# Network diagram with PTDF example
pos = {'Bus1': (0, 1), 'Bus2': (1, 0), 'Bus3': (1, 2)}
# Draw buses
for bus, (x, y) in pos.items():
circle = plt.Circle((x, y), 0.15, color='lightblue', ec='black', linewidth=2)
ax2.add_patch(circle)
bus_type = buses.loc[bus, 'bus_type']
type_str = 'Slack' if bus_type == 3 else 'PQ'
ax2.text(x, y-0.05, bus, ha='center', va='center', fontweight='bold')
ax2.text(x, y+0.05, f'({type_str})', ha='center', va='center', fontsize=8)
# Draw lines with PTDF values for injection at Bus2
injection_bus = 1 # Bus2 index
for line_idx, (_, line) in enumerate(lines.iterrows()):
from_pos = pos[line['from_bus']]
to_pos = pos[line['to_bus']]
# Draw line
ax2.plot([from_pos[0], to_pos[0]], [from_pos[1], to_pos[1]],
'k-', linewidth=2)
# Add PTDF value
mid_x = (from_pos[0] + to_pos[0]) / 2
mid_y = (from_pos[1] + to_pos[1]) / 2
ptdf_val = ptdf[line_idx, injection_bus]
ax2.text(mid_x + 0.1, mid_y, f'PTDF: {ptdf_val:.3f}',
bbox=dict(boxstyle="round,pad=0.3", facecolor="yellow", alpha=0.7))
ax2.set_xlim(-0.5, 1.5)
ax2.set_ylim(-0.5, 2.5)
ax2.set_aspect('equal')
ax2.axis('off')
ax2.set_title(f'PTDF Values for 1 MW Injection at Bus2')
plt.tight_layout()
plt.show()
Generation Shift Factors (GSF)#
Generation Shift Factors represent the sensitivity of line flows to shifting generation from one bus to another. This is particularly useful for redispatch analysis.
Mathematical Derivation of GSF#
Starting with the fundamental relationship between line flows and power injections:
where \(\mathbf{f}\) is the line flow vector and \(\mathbf{p}\) is the net injection vector.
Consider shifting \(\Delta G\) MW of generation from bus \( to bus \). This creates a change in the injection vector:
where \(\mathbf{e}_i\) and \(\mathbf{e}_j\) are unit vectors with 1 at positions \( and \) respectively.
The resulting change in line flows is:
Therefore, the Generation Shift Factor for a unit shift (1 MW) is:
GSF is simply the difference between two PTDF columns. It captures the net effect of removing generation from one location and adding it to another, with the slack bus automatically adjusting to maintain power balance.
def calculate_gsf(ptdf, from_bus_idx, to_bus_idx):
"""
Calculate Generation Shift Factors for shifting generation between two buses.
Parameters:
-----------
ptdf : numpy array
PTDF matrix
from_bus_idx : int
Index of bus losing generation
to_bus_idx : int
Index of bus gaining generation
Returns:
--------
gsf : numpy array
GSF vector showing impact on each line
"""
return ptdf[:, to_bus_idx] - ptdf[:, from_bus_idx]
# Example: Calculate GSF for shifting generation from Bus3 to Bus1
bus_map = {name: i for i, name in enumerate(buses.index)}
from_bus = 'Bus3'
to_bus = 'Bus1'
gsf = calculate_gsf(ptdf, bus_map[from_bus], bus_map[to_bus])
print(f"Generation Shift Factors ({from_bus} → {to_bus}):")
print("=" * 50)
for i, line in enumerate(lines.index):
print(f"{line}: {gsf[i]:.4f}")
print(f"\nInterpretation:")
print(f"Shifting 10 MW from {from_bus} to {to_bus} would change flows by:")
for i, line in enumerate(lines.index):
flow_change = gsf[i] * 10
print(f"{line}: {flow_change:+.2f} MW")
Generation Shift Factors (Bus3 → Bus1):
==================================================
L1: 0.3333
L2: 0.6667
L3: 0.3333
Interpretation:
Shifting 10 MW from Bus3 to Bus1 would change flows by:
L1: +3.33 MW
L2: +6.67 MW
L3: +3.33 MW
The all-positive numbers are correct because shifting the generation from Bus 3 to Bus 1 will cause more flow through all the lines. That is, through L1(1-2), through L2 (1-2) and through L3 (2-3).
Line Outage Distribution Factors (LODF)#
LODF tells us how power flow redistributes when a line is removed from service. The LODF matrix element LODF[l,k] represents the fraction of pre-contingency flow on line k that appears on line l when line k is outaged. This is crucial for N-1 contingency analysis.
Mathematical Derivation of LODF#
When line \(k\) (connecting buses \(m\) and \(n\)) is outaged, its pre-contingency flow \(f_k^0\) must redistribute through the remaining network. We derive LODF using the superposition principle.
Step 1: Model the outage using superposition
Rather than reformulating the entire network without line \(k\), we use superposition:
Keep the original network intact (including line \(k\))
Add compensating injections to force the flow on line \(k\) to zero
This is mathematically equivalent to removing the line but much simpler to compute.
Step 2: Determine the compensating injection
To simulate the outage, we inject power \(P\) at bus \(m\) and withdraw \(P\) at bus \(n\). This injection pattern creates flows throughout the network according to PTDF.
The flow created on line \(k\) by this injection is: $\(\Delta f_k = P \cdot (\text{PTDF}_{k,m} - \text{PTDF}_{k,n})\)$
For the total flow on line \(k\) to be zero (simulating the outage): $\(f_k^0 + \Delta f_k = 0\)$
where \(f_k^0\) is the pre-contingency flow on line \(k\).
Substituting and solving for \(P\): $\(f_k^0 + P \cdot (\text{PTDF}_{k,m} - \text{PTDF}_{k,n}) = 0\)$
Since PTDF is defined for power flowing from \(m\) to \(n\), and noting that \(\text{PTDF}_{k,m} < 1\) (not all power injected at \(m\) flows through line \(k\)), we can rewrite:
Step 3: Calculate the flow redistribution on other lines
The compensating injection \(P\) creates flow changes on all other lines. For line \(l\):
Substituting our expression for \(P\):
Step 4: Define LODF
The Line Outage Distribution Factor is the fraction of the pre-contingency flow on line \(k\) that appears on line \(l\) when line \(k\) is outaged:
Physical interpretation of the denominator: The term \((1 - \text{PTDF}_{k,m} + \text{PTDF}_{k,n})\) is crucial. It represents the “effectiveness” of the compensating injection in canceling flow on line \(k\). If this term were 1, it would mean the injection perfectly maps to flow on line \(k\). Since it’s typically less than 1, we need to scale up the injection accordingly. This is not double counting - it’s the exact scaling needed to achieve zero flow on the outaged line while keeping it mathematically in the network.
def calculate_lodf(ptdf, lines, buses):
"""
Calculate Line Outage Distribution Factors.
Parameters:
-----------
ptdf : numpy array
PTDF matrix
lines : DataFrame
Line data
buses : DataFrame
Bus data
Returns:
--------
lodf : numpy array
LODF matrix where lodf[l,k] is the fraction of flow from line k
that appears on line l when line k is out
"""
n_lines = len(lines)
lodf = np.zeros((n_lines, n_lines))
# Create bus name to index mapping
bus_map = {name: i for i, name in enumerate(buses.index)}
for k in range(n_lines): # Outaged line
# Get buses connected by line k
from_bus_k = bus_map[lines.iloc[k]['from_bus']]
to_bus_k = bus_map[lines.iloc[k]['to_bus']]
# Denominator: 1 - PTDF[k,m] + PTDF[k,n]
# This represents the "self-impedance" of the outaged line
denominator = 1 - ptdf[k, from_bus_k] + ptdf[k, to_bus_k]
if abs(denominator) < 1e-10:
# Handle numerical issues
print(f"Warning: Near-zero denominator for line {k}")
continue
for l in range(n_lines): # Monitored line
if l == k:
# A line cannot carry its own flow when it's out
lodf[l, k] = -1.0
else:
# LODF formula
numerator = ptdf[l, from_bus_k] - ptdf[l, to_bus_k]
lodf[l, k] = numerator / denominator
return lodf
# Calculate LODF for our network
lodf = calculate_lodf(ptdf, lines, buses)
print("LODF Matrix:")
print("(Row = monitored line, Column = outaged line)")
lodf_df = pd.DataFrame(lodf,
index=[f"{l['from_bus']}-{l['to_bus']}" for _, l in lines.iterrows()],
columns=[f"{l['from_bus']}-{l['to_bus']}" for _, l in lines.iterrows()])
print(lodf_df.round(4))
LODF Matrix:
(Row = monitored line, Column = outaged line)
Bus1-Bus2 Bus1-Bus3 Bus2-Bus3
Bus1-Bus2 -1.0 1.0 -1.0
Bus1-Bus3 1.0 -1.0 1.0
Bus2-Bus3 -1.0 1.0 -1.0
Demonstrating LODF with Contingency Analysis#
Let’s demonstrate how LODF is used to quickly assess post-contingency flows without re-running power flow.
def analyze_contingency(base_flows, lodf, lines, outaged_line_idx):
"""
Analyze the impact of a line outage using LODF.
Parameters:
-----------
base_flows : array
Pre-contingency line flows
lodf : array
LODF matrix
lines : DataFrame
Line data
outaged_line_idx : int
Index of line to outage
"""
n_lines = len(lines)
post_flows = base_flows.copy()
# Flow on outaged line redistributes to other lines
outaged_flow = base_flows[outaged_line_idx]
print(f"\nContingency Analysis: Outage of {lines.index[outaged_line_idx]}")
print("=" * 60)
print(f"Pre-contingency flow on outaged line: {outaged_flow:.2f} MW\n")
for l in range(n_lines):
if l == outaged_line_idx:
post_flows[l] = 0 # Outaged line carries no flow
else:
# Post-contingency flow = base flow + LODF * outaged flow
flow_increase = lodf[l, outaged_line_idx] * outaged_flow
post_flows[l] = base_flows[l] + flow_increase
# Display results
results = pd.DataFrame({
'Line': lines.index,
'Base Flow (MW)': base_flows,
'Post-Cont Flow (MW)': post_flows,
'Change (MW)': post_flows - base_flows,
'Limit (MW)': lines['limit'].values,
'Post-Cont Loading (%)': np.abs(post_flows) / lines['limit'].values * 100
})
print(results.round(2))
# Check for overloads
overloaded = results[results['Post-Cont Loading (%)'] > 100]
if len(overloaded) > 0:
print("\n⚠️ WARNING: Post-contingency overloads detected!")
print(overloaded[['Line', 'Post-Cont Flow (MW)', 'Limit (MW)', 'Post-Cont Loading (%)']])
else:
print("\n✓ No post-contingency overloads")
return post_flows
# Example: Calculate base case flows for a dispatch scenario
# Net injections: G1=100MW at Bus1, Load=100MW at Bus2, Load=80MW at Bus3, G3=80MW at Bus3
net_injection = np.array([100, -100, 0]) # Net at each bus
base_flows = ptdf @ net_injection
print("Base Case Flows:")
for i, line in enumerate(lines.index):
print(f"{line}: {base_flows[i]:.2f} MW (Limit: {lines.iloc[i]['limit']} MW)")
# Analyze contingency for each line
for outage_idx in range(len(lines)):
post_flows = analyze_contingency(base_flows, lodf, lines, outage_idx)
Base Case Flows:
L1: 77.78 MW (Limit: 120 MW)
L2: 22.22 MW (Limit: 100 MW)
L3: -22.22 MW (Limit: 80 MW)
Contingency Analysis: Outage of L1
============================================================
Pre-contingency flow on outaged line: 77.78 MW
Line Base Flow (MW) Post-Cont Flow (MW) Change (MW) Limit (MW) \
0 L1 77.78 0.0 -77.78 120
1 L2 22.22 100.0 77.78 100
2 L3 -22.22 -100.0 -77.78 80
Post-Cont Loading (%)
0 0.0
1 100.0
2 125.0
⚠️ WARNING: Post-contingency overloads detected!
Line Post-Cont Flow (MW) Limit (MW) Post-Cont Loading (%)
2 L3 -100.0 80 125.0
Contingency Analysis: Outage of L2
============================================================
Pre-contingency flow on outaged line: 22.22 MW
Line Base Flow (MW) Post-Cont Flow (MW) Change (MW) Limit (MW) \
0 L1 77.78 100.0 22.22 120
1 L2 22.22 0.0 -22.22 100
2 L3 -22.22 -0.0 22.22 80
Post-Cont Loading (%)
0 83.33
1 0.00
2 0.00
✓ No post-contingency overloads
Contingency Analysis: Outage of L3
============================================================
Pre-contingency flow on outaged line: -22.22 MW
Line Base Flow (MW) Post-Cont Flow (MW) Change (MW) Limit (MW) \
0 L1 77.78 100.0 22.22 120
1 L2 22.22 0.0 -22.22 100
2 L3 -22.22 0.0 22.22 80
Post-Cont Loading (%)
0 83.33
1 0.00
2 0.00
✓ No post-contingency overloads
Integration with SCED#
Now let’s demonstrate how to use our calculated PTDF and LODF in a Security-Constrained Economic Dispatch (SCED) problem. This shows the practical application of these sensitivity factors.
def run_sced_with_calculated_ptdf(buses, generators, lines, ptdf, lodf, include_n1=True):
"""
Run SCED using calculated PTDF and optionally include N-1 constraints.
Parameters:
-----------
buses : DataFrame
Bus data
generators : DataFrame
Generator data
lines : DataFrame
Line data
ptdf : array
Calculated PTDF matrix
lodf : array
Calculated LODF matrix
include_n1 : bool
Whether to include N-1 contingency constraints
"""
# Create optimization problem
prob = LpProblem("SCED_with_PTDF", LpMinimize)
# Decision variables: generation
p_gen = {}
for gen_id in generators.index:
p_gen[gen_id] = LpVariable(f"p_{gen_id}", 0, generators.loc[gen_id, 'p_max'])
# Objective: minimize generation cost
prob += lpSum(generators.loc[g, 'cost'] * p_gen[g] for g in generators.index)
# Power balance constraint
total_demand = buses['demand'].sum()
prob += lpSum(p_gen[g] for g in generators.index) == total_demand, "Power_Balance"
# Calculate net injection at each bus
bus_map = {name: i for i, name in enumerate(buses.index)}
net_injection = {}
for bus_name in buses.index:
# Generation at this bus
gen_at_bus = generators[generators['bus'] == bus_name].index
generation = lpSum(p_gen[g] for g in gen_at_bus) if len(gen_at_bus) > 0 else 0
# Net injection = generation - demand
net_injection[bus_name] = generation - buses.loc[bus_name, 'demand']
# Base case line flow constraints using PTDF
line_flows = {}
for line_idx, line_name in enumerate(lines.index):
# Flow = sum(PTDF * net_injection)
flow = lpSum(ptdf[line_idx, bus_map[bus]] * net_injection[bus]
for bus in buses.index)
line_flows[line_name] = flow
# Line limits
limit = lines.iloc[line_idx]['limit']
prob += flow <= limit, f"Line_limit_pos_{line_name}"
prob += flow >= -limit, f"Line_limit_neg_{line_name}"
# N-1 contingency constraints if requested
if include_n1:
for k_idx, k_name in enumerate(lines.index): # Outaged line
for l_idx, l_name in enumerate(lines.index): # Monitored line
if l_idx != k_idx:
# Post-contingency flow = base flow + LODF * outaged flow
post_cont_flow = line_flows[l_name] + lodf[l_idx, k_idx] * line_flows[k_name]
# Post-contingency limits
limit = lines.iloc[l_idx]['limit']
prob += post_cont_flow <= limit, f"N1_pos_{l_name}_out_{k_name}"
prob += post_cont_flow >= -limit, f"N1_neg_{l_name}_out_{k_name}"
# Solve
prob.solve(PULP_CBC_CMD(msg=0))
# Extract results
if prob.status == 1: # Optimal
print(f"\nSCED Results ({'with N-1' if include_n1 else 'without N-1'}):")
print("=" * 50)
print(f"Status: Optimal")
print(f"Total cost: ${value(prob.objective):.2f}")
print(f"LMP: ${prob.constraints['Power_Balance'].pi:.2f}/MWh\n")
print("Generator Dispatch:")
for g in generators.index:
gen_value = value(p_gen[g])
print(f" {g} at {generators.loc[g, 'bus']}: {gen_value:.1f} MW")
print("\nLine Flows:")
for line_idx, line_name in enumerate(lines.index):
flow = value(line_flows[line_name])
limit = lines.iloc[line_idx]['limit']
loading = abs(flow) / limit * 100
print(f" {line_name}: {flow:.1f} MW / {limit} MW ({loading:.1f}% loaded)")
else:
print(f"Optimization failed: {LpStatus[prob.status]}")
return prob
# Run SCED without N-1 constraints
print("Running SCED without N-1 constraints...")
prob_base = run_sced_with_calculated_ptdf(buses, generators, lines, ptdf, lodf, include_n1=False)
# Run SCED with N-1 constraints
print("\n" + "="*60)
print("Running SCED with N-1 constraints...")
prob_n1 = run_sced_with_calculated_ptdf(buses, generators, lines, ptdf, lodf, include_n1=True)
Running SCED without N-1 constraints...
SCED Results (without N-1):
==================================================
Status: Optimal
Total cost: $3600.00
LMP: $20.00/MWh
Generator Dispatch:
G1 at Bus1: 180.0 MW
G2 at Bus1: 0.0 MW
G3 at Bus3: 0.0 MW
Line Flows:
L1: 104.4 MW / 120 MW (87.0% loaded)
L2: 75.6 MW / 100 MW (75.6% loaded)
L3: 4.4 MW / 80 MW (5.6% loaded)
============================================================
Running SCED with N-1 constraints...
Optimization failed: Infeasible
Summary and Utilities for Reuse#
We’ve developed a complete framework for calculating PTDF, GSF, and LODF from network topology. These tools are essential for:
Security-constrained economic dispatch (SCED)
Contingency analysis
Transmission planning
Real-time market operations
Let’s package the key functions for easy reuse in other notebooks.
Conclusion#
This notebook has provided a complete implementation of PTDF, GSF, and LODF calculation from network topology data. The key takeaways are:
PTDF tells us how power injections affect line flows and is fundamental to all linearized power system analysis
GSF helps analyze generation redispatch by showing the impact of shifting generation between buses
LODF enables fast contingency analysis by predicting post-outage flows without re-solving power flow
These sensitivity factors make SCED computationally tractable even with N-1 security constraints
The functions developed here can be directly imported and used in the power-system-optimization notebooks, replacing hardcoded values with dynamically calculated ones based on actual network topology.
