Time Series Data Analysis-2#
Month-to-Month Analysis#
In this section, we explore how values change from one month to the next, allowing us to detect seasonality and short-term patterns.
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
from datetime import datetime, timedelta
import numpy as np
!git submodule update --init --recursive
Monthly data Aggregation#
We prompt the user to specify a year (16–18) and a month (e.g., 1–12 for January to December).
Construct a file path dynamically to load the corresponding CSV file containing the time-series data for all the months of given year.
The selected data is then read into a pandas dataframe (df), which becomes the basis for further analysis.
import os
current_dir = os.getcwd()
data_dir = "solar-data/pv-data"
file_path18 = []
file_path17 = []
file_path16 = []
for j in range(12):
file_path18.append(os.path.join(current_dir, data_dir, f"f 2018 {j+1}.csv"))
file_path17.append(os.path.join(current_dir, data_dir, f"f 2017 {j+1}.csv"))
file_path16.append(os.path.join(current_dir, data_dir, f"f 2016 {j+1}.csv"))
import pandas as pd
dtype_dict = {
'f': 'float32' # Convert numeric columns to float32 to reduce memory usage
}
df18 = [pd.read_csv(file, dtype=dtype_dict) for file in file_path18]
df17 = [pd.read_csv(file, dtype=dtype_dict) for file in file_path17]
df16 = [pd.read_csv(file, dtype=dtype_dict) for file in file_path16]
df = [df16,df17,df18]
#For which year would you like a month to month analysis?(16 - 18)
var=16
dff = df[var - 16]
months = ['January', 'February', 'March', 'April', 'May', 'June',
'July', 'August', 'September', 'October', 'November', 'December']
Metrics Calculation#
Mean: The average value of the frequency variable (f) for all the months in the selected year.
Standard Deviation: The variability of the frequency data around the mean.
Skewness: The asymmetry of the frequency distribution.
mean = []
for i in range(12):
alt = dff[i]
mean.append(alt['f'].mean())
print(f'The MEAN of the months in year 20{var} from January to December is:')
mean
The MEAN of the months in year 2016 from January to December is:
[50.000126,
49.999954,
49.999332,
49.999886,
49.999596,
49.99984,
49.99971,
49.99976,
49.999607,
50.00025,
49.99959,
49.999355]
stdev = []
for i in range(12):
alt = dff[i]
stdev.append(alt['f'].std())
print(f'The STANDARD DEVIATION of the months in year 20{var} from January to December is:')
stdev
The STANDARD DEVIATION of the months in year 2016 from January to December is:
[0.055868156,
0.054133136,
0.056034606,
0.059400223,
0.05720208,
0.05436331,
0.055509906,
0.052781273,
0.0532314,
0.05495323,
0.056555677,
0.05530752]
skew = []
for i in range(12):
alt = dff[i]
skew.append(alt['f'].skew())
print(f'The SKEWNESS of the months in year 20{var} from January to December is:')
skew
The SKEWNESS of the months in year 2016 from January to December is:
[0.18413661,
0.17962934,
0.16257153,
0.21715383,
0.1926185,
0.17057034,
0.18004876,
0.24801944,
0.30347863,
0.18840456,
0.15077758,
0.13207896]
Visualization#
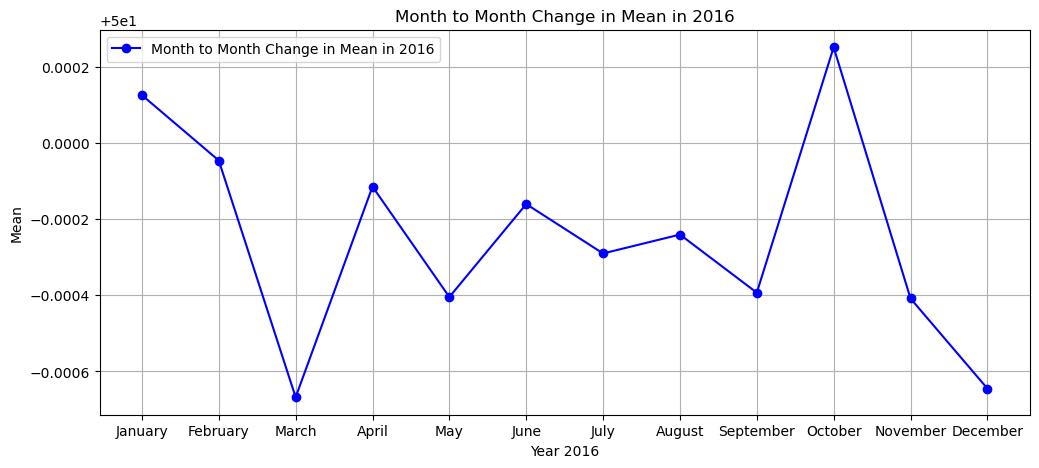
Clear month to month changes of mean, standard deviation and skewness for the given year to visualize changes within the year.
plt.figure(figsize=(12, 5))
plt.plot(months[0:], mean[0:], marker='o', color='b', linestyle='-', label=f'Month to Month Change in Mean in 20{var}')
plt.xlabel(f'Year 20{var}')
plt.ylabel('Mean')
plt.title(f'Month to Month Change in Mean in 20{var}')
plt.grid(True)
plt.legend()
plt.show()
plt.figure(figsize=(12, 5))
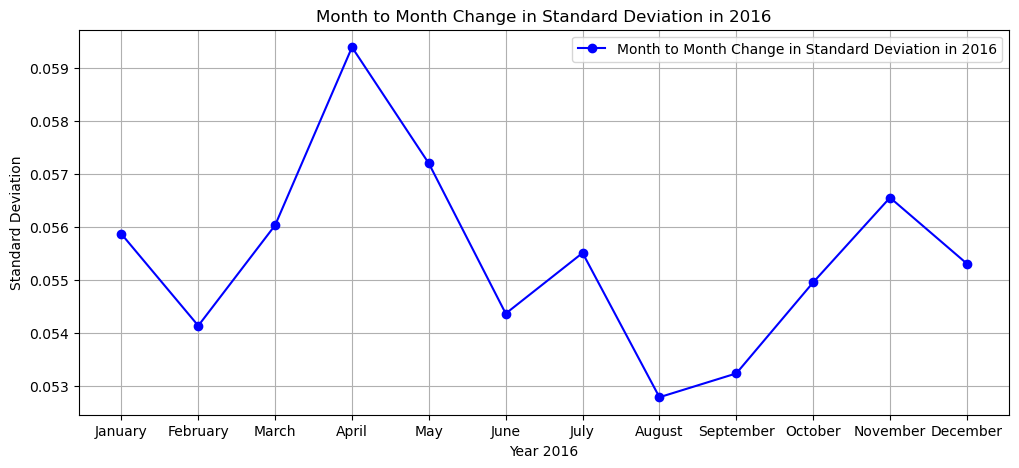
plt.plot(months[0:], stdev[0:], marker='o', color='b', linestyle='-', label=f'Month to Month Change in Standard Deviation in 20{var}')
plt.xlabel(f'Year 20{var}')
plt.ylabel('Standard Deviation')
plt.title(f'Month to Month Change in Standard Deviation in 20{var}')
plt.grid(True)
plt.legend()
plt.show()
plt.figure(figsize=(12, 5))
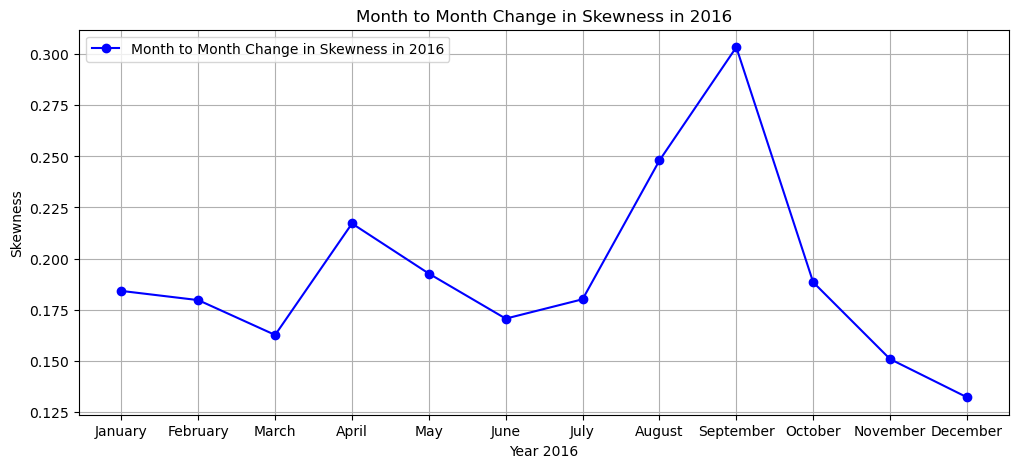
plt.plot(months[0:], skew[0:], marker='o', color='b', linestyle='-', label=f'Month to Month Change in Skewness in 20{var}')
plt.xlabel(f'Year 20{var}')
plt.ylabel('Skewness')
plt.title(f'Month to Month Change in Skewness in 20{var}')
plt.grid(True)
plt.legend()
plt.show()
Crosstables#
Crosstables for metrics such as mean, standard deviation, skewness and CPS1 score for all the months and years are created.
They provide an overview of how specific metrics change over months within a year and allow easy year-to-year comparisons.
mean_v = []
std_dev = []
sk_ew =[]
for j in range(3):
for i in range(12):
alt = df[j][i]
mean_v.append(alt['f'].mean())
std_dev.append(alt['f'].std())
sk_ew.append(alt['f'].skew())
df_10min = []
for j in range(3):
print(f"Processing year {2016+1}")
for i in range(12):
print(f"- Processing month {i+1}")
df[j][i]['dtm'] = pd.to_datetime(df[j][i]['dtm'], utc=True)
df_10min.append(df[j][i].resample('10min', on='dtm').mean())
Processing year 2017
- Processing month 1
- Processing month 2
- Processing month 3
- Processing month 4
- Processing month 5
- Processing month 6
- Processing month 7
- Processing month 8
- Processing month 9
- Processing month 10
- Processing month 11
- Processing month 12
Processing year 2017
- Processing month 1
- Processing month 2
- Processing month 3
- Processing month 4
- Processing month 5
- Processing month 6
- Processing month 7
- Processing month 8
- Processing month 9
- Processing month 10
- Processing month 11
- Processing month 12
Processing year 2017
- Processing month 1
- Processing month 2
- Processing month 3
- Processing month 4
- Processing month 5
- Processing month 6
- Processing month 7
- Processing month 8
- Processing month 9
- Processing month 10
- Processing month 11
- Processing month 12
for i in range(len(df_10min)):
df_10min[i]['del_f'] = df_10min[i]['f'] - 50
cps1 = []
df1_10min = df_10min
e1 = 0.12
for i in range(len(df1_10min)):
cps_ratio = df1_10min[i]['del_f'] * df1_10min[i]['del_f'] / (e1 ** 2)
cps = (2 - cps_ratio)*100
cps1.append(cps.to_frame(name='cps'))
mean_cps1 = []
meancps1 = 0
i = 0
for i in range(len(df1_10min)):
mean_cps1.append(cps1[i]['cps'].mean())
start_date = datetime(2016, 1, 1)
end_date = datetime(2018, 12, 1)
date_list = []
while start_date <= end_date:
date_str = start_date.strftime('%B %Y')
date_list.append(date_str)
start_date += timedelta(days=31)
start_date = start_date.replace(day=1)
years = list(range(2016, 2019))
months = ['Jan', 'Feb', 'Mar', 'Apr', 'May', 'Jun', 'Jul', 'Aug', 'Sep', 'Oct', 'Nov', 'Dec']
data = {
'Year': np.repeat(years, len(months)),
'Month': months * len(years),
'Mean': mean_v,
'Standard Deviation': std_dev,
'Skewness': sk_ew,
'CPS1 score': mean_cps1
}
dff = pd.DataFrame(data)
mean_crosstable = dff.pivot(index='Month', columns='Year', values='Mean')
std_crosstable = dff.pivot(index='Month', columns='Year', values='Standard Deviation')
skew_crosstable = dff.pivot(index='Month', columns='Year', values='Skewness')
cps1_crosstable = dff.pivot(index='Month', columns='Year', values='CPS1 score')
mean_crosstable_str = mean_crosstable.to_string()
std_crosstable_str = std_crosstable.to_string()
skew_crosstable_str = skew_crosstable.to_string()
cps1_crosstable_str = cps1_crosstable.to_string()
pd.set_option('display.max_columns', None)
pd.set_option('display.width', None)
print("Mean Crosstable:")
print(mean_crosstable_str)
Mean Crosstable:
Year 2016 2017 2018
Month
Apr 49.999886 49.999542 50.000671
Aug 49.999760 49.999725 49.999870
Dec 49.999355 49.999798 50.000088
Feb 49.999954 49.999676 49.999046
Jan 50.000126 49.999775 49.998268
Jul 49.999710 49.999832 49.999409
Jun 49.999840 49.999714 50.000587
Mar 49.999332 49.999691 49.998421
May 49.999596 49.999458 49.998764
Nov 49.999592 49.999886 49.999401
Oct 50.000252 49.999844 50.000671
Sep 49.999607 49.999912 49.999363
print("Standard Deviation Crosstable:")
print(std_crosstable_str)
Standard Deviation Crosstable:
Year 2016 2017 2018
Month
Apr 0.059400 0.057603 0.065470
Aug 0.052781 0.059625 0.066557
Dec 0.055308 0.060521 0.065476
Feb 0.054133 0.062952 0.066638
Jan 0.055868 0.057272 0.063057
Jul 0.055510 0.058447 0.066160
Jun 0.054363 0.058637 0.065116
Mar 0.056035 0.061541 0.066643
May 0.057202 0.057244 0.061135
Nov 0.056556 0.062230 0.070056
Oct 0.054953 0.065040 0.069178
Sep 0.053231 0.060592 0.068534
print("\nSkewness Crosstable:")
print(skew_crosstable_str)
Skewness Crosstable:
Year 2016 2017 2018
Month
Apr 0.217154 0.135294 0.173611
Aug 0.248019 0.160047 0.080792
Dec 0.132079 0.143847 0.027416
Feb 0.179629 0.175180 0.210985
Jan 0.184137 0.141553 0.192764
Jul 0.180049 0.167786 0.132517
Jun 0.170570 0.242695 0.225854
Mar 0.162572 0.155781 0.258984
May 0.192619 0.162235 0.274101
Nov 0.150778 0.084164 0.065809
Oct 0.188405 0.214123 0.031424
Sep 0.303479 0.220359 0.103189
print("\nCPS1 score Crosstable:")
print(cps1_crosstable_str)
CPS1 score Crosstable:
Year 2016 2017 2018
Month
Apr 183.996201 184.516281 181.385391
Aug 186.952255 183.442032 181.345306
Dec 185.348511 182.996033 180.037445
Feb 185.683640 181.742096 180.694016
Jan 184.723755 184.840958 182.318665
Jul 186.201004 184.388245 182.062576
Jun 187.295776 183.947220 181.632950
Mar 185.523132 182.429382 179.868927
May 185.692612 184.486923 182.894455
Nov 185.200119 183.108994 177.509521
Oct 186.462555 181.964569 178.959198
Sep 185.969696 183.100433 179.720093
Purpose of month-to-month analysis#
Comparative Analysis:
Allow quick comparisons between months within the same year.
Enable cross-year comparisons for the same month (e.g., January 2016 vs. January 2018).
Trend Identification:
Help identify long-term trends, such as:
Increasing variability (standard deviation) over years.
Changes in distribution symmetry (skewness) over time.
Seasonal or cyclical patterns in frequency (e.g., high means in summer months).
Summarized Insights:
Provide a clear, high-level summary of key metrics without requiring extensive manual exploration of raw data.
Yearly Data Aggegration#
Data for each year (2016–2018) is stored as separate dataframes (df_2016, df_2017, etc.).
Monthly data within each year is concatenated to create a complete yearly dataset.
All yearly datasets are appended to a list yearsData for easier iteration and analysis.
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
df_2018 = pd.concat(df18).reset_index(drop=True)
df_2017 = pd.concat(df17).reset_index(drop=True)
df_2016 = pd.concat(df16).reset_index(drop=True)
yearsData =[]
yearsData.append(df_2016)
yearsData.append(df_2017)
yearsData.append(df_2018)
Computation of Metrics:#
For each year, the following statistics are calculated:
Mean
Standard Deviation
Skewness
The yearly mean, standard deviation, and skewness are displayed in ascending order for quick inspection.
mean = []
for i in range(3):
var = yearsData[i]
mean.append(var['f'].mean())
print('The MEAN of the yearly data from 2016 to 2018 in ascending order is:')
mean
The MEAN of the yearly data from 2016 to 2018 in ascending order is:
[49.999775, 49.9998, 49.999474]
stdev = []
for i in range(3):
var1 = yearsData[i]
stdev.append(var1['f'].std())
print('The STANDARD DEVIATION of the yearly data from 2016 to 2018 in ascending order is:')
stdev
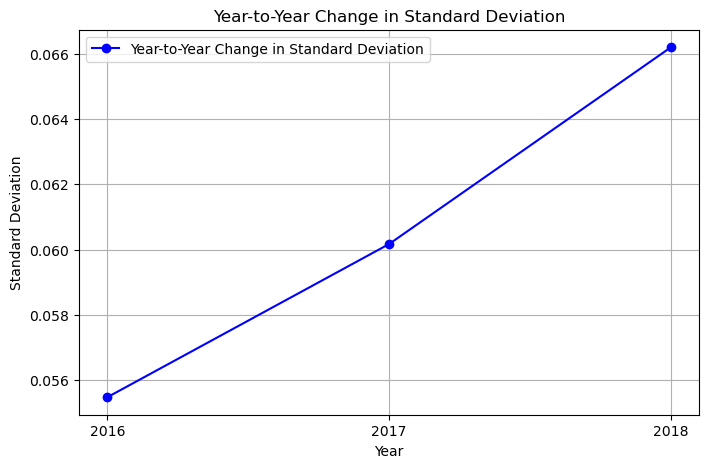
The STANDARD DEVIATION of the yearly data from 2016 to 2018 in ascending order is:
[0.05547456, 0.060169745, 0.0661998]
skew = []
for i in range(3):
var2 = yearsData[i]
skew.append(var2['f'].skew())
print('The SKEWNESS of the yearly data from 2016 to 2018 in ascending order is:')
skew
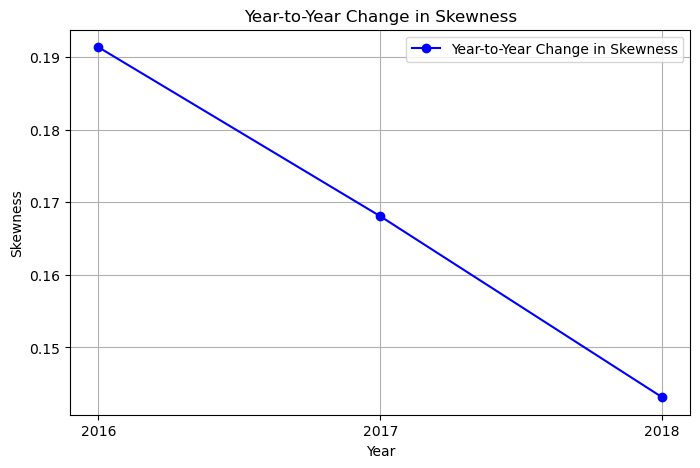
The SKEWNESS of the yearly data from 2016 to 2018 in ascending order is:
[0.1913346, 0.16806537, 0.14315064]
years = ['2016','2017','2018']
Visualization of Yearly Trends#
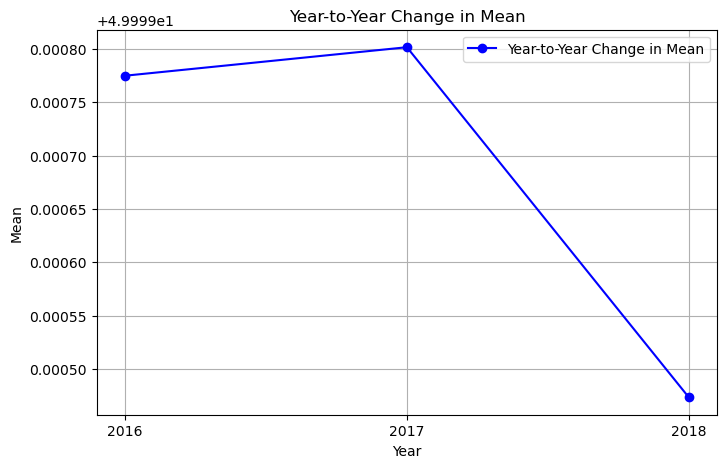
Three separate line plots are created to illustrate:
Changes in mean over the years.
Trends in standard deviation across years.
Variations in skewness across the dataset for each year.
These plots help visualize how the frequency variable (f) evolves from 2016 to 2018.
plt.figure(figsize=(8, 5))
plt.plot(years[0:], mean[0:], marker='o', color='b', linestyle='-', label='Year-to-Year Change in Mean')
plt.xlabel('Year')
plt.ylabel('Mean')
plt.title('Year-to-Year Change in Mean')
plt.grid(True)
plt.legend()
plt.show()
plt.figure(figsize=(8, 5))
plt.plot(years[0:], stdev[0:], marker='o', color='b', linestyle='-', label='Year-to-Year Change in Standard Deviation')
plt.xlabel('Year')
plt.ylabel('Standard Deviation')
plt.title('Year-to-Year Change in Standard Deviation')
plt.grid(True)
plt.legend()
plt.show()
plt.figure(figsize=(8, 5))
plt.plot(years[0:], skew[0:], marker='o', color='b', linestyle='-', label='Year-to-Year Change in Skewness')
plt.xlabel('Year')
plt.ylabel('Skewness')
plt.title('Year-to-Year Change in Skewness')
plt.grid(True)
plt.legend()
plt.show()
Conclusion#
We have built a powerful tool for exploring, analyzing, and visualizing frequency data. By combining user interactivity, detailed analysis, and aggregated insights, it provides a flexible and reusable framework for understanding time-series data across multiple timeframes.
